Baccalaurat ES - Oral de rattrapage

Vous trouverez sur cette page un ensemble d’exercices typiques de l’oral de rattrapage de mathématiques de la série ES. Pour chaque exercice, une correction détaillée et commentée est proposée.

Informations relatives au déroulement de l’épreuve orale

• L’épreuve orale est constituée d’une préparation de 20 minutes suivie d’un entretien de la même durée.
• L’utilisation de la calculatrice est autorisée.
• Le candidat ne peut utiliser que le brouillon fourni par l’examinateur.
• La qualité des raisonnements, de l’expression et la précision des justifications prendront une part importante dans l’appréciation.
• Il s’agit d’une épreuve orale, il n’est donc pas indispensable de rédiger sur votre feuille le détail de chaque réponse. Par contre, le candidat doit être capable d’apporter toutes les justifications nécessaires et demandées lors de l’interrogation orale.
• Le sujet comporte deux exercices qui doivent être traités tous les deux dans l’ordre que le candidat choisit.
• Des consignes ou des questions supplémentaires pourront être oralement proposées par l’examinateur.

Exercices communs à tous les candidats

QCM avec lecture graphique : dérivée, convexité et primitive

On considère une fonction $f$ définie sur $[-2\,;4]$ dont la courbe représentative $\mathscr{C}$ est donnée ci dessous.

Les droites $(d_1)$ et $(d_2)$ sont tangentes à $\mathscr{C}$ respectivement au point $A$ d’abscisse $-1$ et au point $B$ d’abscisse $1$.

Pour chaque question suivante déterminer la seule réponse exacte. Justifier la réponse.

• Question 1. $\,$ La fonction $f$ est concave sur l’intervalle :

  a. $\,[-2\,;0]$

  b. $\,[-1\,;2]$

  c. $\,[2\,;3]$

  Réponse attendue

  Réponse a. FAUX

  $(d_1)$, tangente à $\mathscr{C}$ au point d’abscisse $-1$, est située en dessous de $\mathscr{C}$. Donc sur l’intervalle $[-2\,;0]$, il existe au au moins une tangente située en dessous de $\mathscr{C}$. Donc $f$ n’est pas concave sur cet intervalle.

  Réponse b. FAUX

  La justification est la même que pour la réponse b.

  Réponse c. VRAI

  Les deux réponses précédentes étant fausses, la réponse c. ne peut qu’être vrai. Remarque. Intuitivement, on voit que la courbe a une forme de “U renversé” sur l’intervalle $[1\,;4]$. On pouvait donc conjecturer que $f$ est concave sur l’intervalle $[1\,;4]$ et en particulier sur l’intervalle $[2\,;3]$ contenu dans l’intervalle précédent.

• Question 2. $\,$ Le nombre dérivé de $f'(1)$ est égal à :

  a. $\,0$

  b. $\,2$

  c. $\,3$

  Réponse attendue

  Le nombre dérivé $f'(1)$ est égal à la pente de la tangente à $\mathscr{C}$ au point s’abscisse 1, c’est-a-dire la pente de $(d_1)$.

  On détermine graphiquement la pente de $(d_1)$. Pour cela :

  Méthode 1.

  • On repère les points de la grille situés sur la droite $(d_1)$. Ici, il s’agit du point $B$ et des points $C$ et $D$ ajoutés sur la figure ci-dessous :

  

  • On trace l’ “escalier”. Ici cet escalier a une marche horizontale de $1$ ($\Delta x = 1$) et une marche verticale de $+3$ ($\Delta y = +3$).

  Remarque.

  Attention, ici la marche verticale $\Delta y$ est positive car la droite $(d_1)$ “monte” de la gauche vers la droite. Si la droite “descendait” de la gauche vers la droite, la marche verticale serait négative.

  • On calcule la pente :

  $$\begin{align*} f'(1) &= \text{pente}(d_1) \\ &= \frac{\Delta y}{\Delta x} \\ &= \frac{+3}{1} \\ &= 3 \end{align*}$$

  Méthode 2.

  La droite $(d_1)$ passe par les points $B\,(1\,;2)$ et $C\,(2\,;5)$. Donc :

  $$\begin{align*} f'(1) &= \text{pente}(d_1) \\ &= \frac{\Delta y}{\Delta x} \\ &= \frac{y_C - y_B}{x_C - x_B} \\ &= \frac{5 - 2}{2 - 1} \\ &= \frac{+3}{1} \\ &= 3 \end{align*}$$

  Conclusion. La réponse VRAI est donc la réponse c.

• Question 3. $\,$ Le courbe $\mathscr{C}$ admet un point d’inflexion au point d’abscisse :

  a. $\,0$

  b. $\,1$

  c. $\,2$

  Réponse attendue

  $(d_2)$ tangente à $\mathscr{C}$ au point $B$ coupe la courbe $\mathscr{C}$ au point $B$. Donc le point $B$ d’abscisse $1$ est un point d’inflexion de $\mathscr{C}$.

  La réponse VRAI est donc la réponse c.

• Question 4. $\,$ Une primitive $F$ de la fonction $f$ sur $[-2\,;5]$ est décroissante sur l’intevalle :

  a. $\,[-2\,;0]$

  b. $\,[1\,;2]$

  c. $\,[3\,;4]$

  Réponse attendue

  Sur tout intervalle, si $F$ est décroissante alors sa dérivée $f$ doit être négative. Autrement dit la courbe $\mathscr{C}$ doit être située au dessous de l’axe des abscisses. Ce n’est vrai que sur l’intervalle $[3\,;4]$.

  La réponse VRAI est donc la réponse c.

Fonction exponentielle sans intégrale, calculatoire

Soit $f$ la fonction définie sur l’intervalle $[-1 ; 10]$ par $f(x) = (2x + 1)\text{e}^{-x}$. On note $f'$ la fonction dérivé de $f$.

1. Déterminer l’expression de $f'(x)$ et montrer que $f'(x) = (1 - 2x)\text{e}^{-x}$ . Indication. En cas de blocage, admettre le résultat de cette question pour continuer l’exercice.

   Réponse attendue

   On pose :

   • $u(x) = 2x + 1$
   • $v(x) = \text{e}^{-x}$

   On a donc :

   • $u'(x) = 2$
   • $v'(x) = -\text{e}^{-x}$

   On applique ensuite la formule de la dérivée d’un produit :

   $$\begin{align*} f'(x) &= (u \cdot v)'(x) \\ &= \big( u' \cdot v + u \cdot v' \big)(x) \\ &= 2\text{e}^{-x} + (2x + 1)(-\text{e}^{-x}) \\ &= 2\text{e}^{-x} + (-2x - 1)\text{e}^{-x} \\ &= (1 - 2x)\text{e}^{-x} \end{align*}$$

2. Étudier le signe de $f'(x)$ et dresser le tableau de variation de $f$.

   Réponse attendue

   Pour tout $x \in [-1;10]$, $\quad \text{e}^{-x} > 0$. Donc $f'(x)$ a le même signe que le polynôme du premier degré $1 - 2x$.

   	$1 - 2x \:$	$= 0$
   $\iff \quad$	$-2x \:$	$= -1$
   $\iff \quad$	$x \:$	$= 0{,}5$

   $1 - 2x$ s’annule en $0{,}5$ et son coefficient dominant est $-2 < 0$. On en déduit :

   

   Calcul des images :

   $$\begin{align*} f(-2) &= \big(2 \cdot (-1) + 1\big)\text{e}^{-(-1)} \\ &= -\text{e} \\ &= -2{,}71 \cdots \\ &\simeq -2{,}7 \quad (\text{Arrondi à }0{,}1) \end{align*}$$

   
   

   $$\begin{align*} f(0{,}5) &= \big(2 \cdot 0{,}5 + 1\big)\text{e}^{-0{,}5} \\ &= 2\text{e}^{-0{,}5} \\ &= \frac{2}{\text{e}^{0{,}5}} \\ &= \frac{2}{\sqrt{\text{e}}} \\ &= 1{,}21 \cdots \\ &\simeq 1{,}2 \quad (\text{Arrondi à }0{,}1) \end{align*}$$

   
   

   $$\begin{align*} f(10) &= \big(2 \cdot 10 + 1\big)\text{e}^{-10} \\ &= 21\text{e}^{-10} \\ &= 9{,}5 \cdots \times 10^{-4} \\ &= 0{,}00095 \cdots \\ &\simeq 0{,}0 \quad (\text{Arrondi à }0{,}1) \end{align*}$$

   Remarque.

   A l’oral n’hésitez pas à gagner du temps en obtenant directement à la calculatrice les valeurs approchées des images (en général au dixième). L’examinateur pourra cependant vous demander le calcul d’une valeur exacte pendant l’entretien.

3. En déduire le maximum de la fonction $f$ et pour quelle valeur de $x$ il est atteint.

   Réponse attendue

   Le maximum de $f$ vaut $\dfrac{2}{\sqrt{\text{e}}}$ soit environ $1{,}2$ arrondi au dixième. Ce maximum est atteint pour $x = 0{,}5$.

4. Montrer que l’équation $f(x) = -1$ admet une seule solution.

   Réponse attendue

   On commence par compléter le tableau de variation fait à la question 2. :

   

   Étape 1 : sur l’intervalle $[-1\,;0{,}5]$

   • $f$ est continue et strictement croissante.
   • $f(-1) \simeq -2{,}7$
   • $f(0{,}5) \simeq 1{,}2$
   • $-1 \in [-2{,}7\,;1{,}2]$

   Donc d’après le corolaire du TVI, l’équation $f(x) = -1$ admet une unique solution $\alpha$ sur l’intervalle $[-1\,;0{,}5]$.

   
   

   Étape 2 : sur l’intervalle $[0{,}5\,;10]$

   $f$ est continue et strictement décroissante. Donc le minimum de $f$ sur cet intervalle est $f(10) \simeq 0{,}0 > -1$. Donc l’équation $f(x) = -1$ n’admet aucune solution sur l’intervalle $[0{,}5\,;10]$.

   
   

   Étape 3 : Bilan

   Donc l’équation $f(x) = -1$ admet une unique solution $\alpha$ avec $\alpha \in [-1\,;0{,}5]$.

Fonction exponentielle sans intégrale, calculatoire

Le bénéfice en millions d’euros, réalisé par une entreprise lorsqu’elle produit et vend $x$ milliers d’objets, $0\leq x \leq 8\,$, est donné par la fonction $B$ définie sur $[0\,; 8]$ par :

$$\begin{align*} B(x) = (20x + 10)\text{e}^{-0{,}5x} - 10 \end{align*}$$

On note $B'$ la fonction dérivée de $B$.

1. Déterminer l’expression de $B'(x)$ et montrer que :

   $$\begin{align*} B'(x) = (15 - 10x)\text{e}^{-0{,}5x} \end{align*}$$

   Indication. En cas de blocage, admettre le résultat de cette question pour continuer l’exercice.

   Réponse attendue

   Remarque

   La dérivée d’une somme est égale à la somme des dérivées. Donc la constante $-10$ va “disparaître” à la dérivation. Il suffit donc simplement de l’ignorer pour dériver $B$. On se concentre donc uniquement sur la partie suivante de l’expression de la fonction $B$ :

   $$\begin{align*} (20x + 10)\text{e}^{-0{,}5x} \end{align*}$$

   On pose :

   • $u(x) = 20x + 10$
   • $v(x) = \text{e}^{-0{,}5x}$

   On a donc :

   • $u'(x) = 20$
   • $v'(x) = -0{,}5\text{e}^{-0{,}5x}$

   On applique ensuite la formule de la dérivée d’un produit :

   $$\begin{align*} f'(x) &= (u \cdot v)'(x) \\ &= \big( u' \cdot v + u \cdot v' \big)(x) \\ &= 20\text{e}^{-0{,}5x} + (20x + 10)(-0{,}5)\text{e}^{-0{,}5x} \\ &= 20\text{e}^{-0{,}5x} + (-10x - 5)\text{e}^{-0{,}5x} \\ &= (15 - 10x)\text{e}^{-0{,}5x} \end{align*}$$

2. Étudier le signe de $B'(x)$ et dresser le tableau de variation de $B$.

   Réponse attendue

   Pour tout $x \in [0\,; 8]$, $\; \text{e}^{-0{,}5x} > 0$. Donc $B'(x)$ a le même signe que le polynôme du premier degré $15 - 10x$.

   	$15 - 10x \:$	$= 0$
   $\iff \quad$	$-10x \:$	$= -15$
   $\iff \quad$	$x \:$	$= \dfrac{-15}{-10}$
   $\iff \quad$	$x \:$	$= 1{,}5$

   $15 - 10x$ s’annule en $1{,}5$ et son coefficient dominant est $-10 < 0$. On en déduit :

   

   Calcul des images :

   $$\begin{align*} f(0) &= (20 \cdot 0 + 10)\text{e}^{-0{,}5\cdot 0} - 10 \\ &= 10\text{e}^0 - 10\\ &= 10 - 10 \\ &= 0 \\ \end{align*}$$

   
   

   $$\begin{align*} f(1{,}5) &= (20 \cdot 1{,}5 + 10)\text{e}^{-0{,}5\cdot 1{,}5} - 10 \\ &= 40\text{e}^{-0{,}75} - 10\\ &= 8{,}89 \cdots \\ &\simeq 8{,}9 \quad (\text{Arrondi à }0{,}1) \\ \end{align*}$$

   
   

   $$\begin{align*} f(8) &= (20 \cdot 8 + 10)\text{e}^{-0{,}5\cdot 8} - 10 \\ &= 170\text{e}^{-4} - 10\\ &= -6{,}88\cdots \\ &\simeq -6{,}9\\ \end{align*}$$

   Remarque.

   A l’oral n’hésitez pas à gagner du temps en obtenant directement à la calculatrice les valeurs approchées des images (en général au dixième). L’examinateur pourra cependant vous demander le calcul d’une valeur exacte pendant l’entretien.

3. En déduire le nombre d’objets à produire et à vendre pour que l’entreprise réalise un bénéfice maximal. Préciser la valeur de ce bénéfice maximal.

   Réponse attendue

   D’après le tableau de variation, le maximum de $B$ vaut environ $8{,}9$ et il est atteint pour $x = 1{,}5$. Donc pour que l’entreprise réalise un bénéfice maximal, elle doit produire et vendre $1\,500$ objets. Le bénéfice maximal est alors d’environ $8{,}9$ millions d’Euros.

4. Facultatif. Montrer que l’équation $B(x) = -1$ admet une seule solution. Donner une valeur approchée à $10^{-3}$ de cette solution. Interpréter ce résultat dans le contexte de l’exercice.

   Réponse attendue

   On commence par compléter le tableau de variation fait à la question 2. :

   

   Étape 1 : sur l’intervalle $[0\,;1{,}5]$

   $B$ est continue et strictement croissante. Donc le minimum de $B$ sur cet intervalle est $B(0) = 0 > -1$. Donc l’équation $B(x) = -1$ n’admet aucune solution sur l’intervalle $[0\,;1{,}5]$.

   
   

   Étape 2 : sur l’intervalle $[1{,}5\,;8]$

   • $B$ est continue et strictement décroissante.
   • $B(1{,}5) \simeq 8{,}9$
   • $B(0{,}5) \simeq -6{,}9$
   • $-1 \in [-6{,}9\,;8{,}9]$

   Donc d’après le corolaire du TVI, l’équation $B(x) = -1$ admet une unique solution $\alpha$ sur l’intervalle $[1{,}5\,;8]$.

   
   

   Étape 3 : Bilan sur l’intervalle $[0\,;8]$

   Donc l’équation $B(x) = -1$ admet une unique solution $\alpha$ avec $\alpha \in [1{,}5\,;8]$.

   À la calculatrice, on obtient : $\quad 5{,}0102 < \alpha < 5,0103$

   Donc : $\quad \alpha \simeq 5{,}010 \quad$ (Arrondi à $10^{-3}$)

   
   

   Interprétation. Donc l’entreprise perd un million d’euros lorsqu’elle produit et vend $5010$ objets.

Suite géométrique avec algorithme

En 2014, une personne place $30\,000$ Euros sur un compte rémunéré au taux annuel de $2\%$, les intérêts étant composés. Pour tout entier naturel $n$, on note $u_n$ la somme disponible au bout de $n$ années de placement. Ainsi, $u_0 = 30\,000$.

1. Exprimer pour tout entier naturel $n$, $u_{n + 1}$ en fonction de $u_n$.

   Réponse attendue

   Tous les ans la somme disponible sur le compte augmente de $t = 2\%$ donc est mutipliée par :

   $$\begin{align*} CM &= 1 + t \\ &= 1 + 0{,}02 \\ &= 1{,}02 \\ \end{align*}$$

   Donc, pour tout entier naturel $n$, $\quad u_{n + 1} = 1{,}02u_n$.

2. On considère l’algorithme ci-dessous. Interpréter la valeur affichée en sortie.

   Variables : $\quad$ $N$ est un nombre entier naturel $\quad$ $U$ est un nombre réel Initialisation : $\quad$ $N$ prend la valeur $0$ $\quad$ $U$ prend la valeur $30000$ Traitement : $\quad$ Tant que $U < 45000$ faire $\quad$ $\quad$ $U$ prend la valeur $1{,}02U$ $\quad$ $\quad$ $N$ prend la valeur $N + 1$ $\quad$ Fin tant que Sortie : $\quad$ Afficher $N$

   Réponse attendue

   L’algorithme renvoie le rang $n$ de l’année à partir de laquelle la somme disponible $u_n$ va dépasser $45\,000$ Euros.

3. En quelle année la somme initiale aura-t-elle augmenté de $50\%$ ?

   Réponse attendue

   La moitié de la somme initiale de $30\,000$ Euros est $15\,000$ Euros. Donc après une augmentation de $50\%$, la somme disponible sera égale à $45\,000$ Euros.

   On doit donc déterminer en quelle année la somme initiale aura atteint $45\,000$ Euros. Deux méthodes sont possibles.

   
   

   Méthode 1. En codant l’algorithme dans une calculatrice

   On donne ci-dessous l’algorithme précédent codé en Ti-Basic, le langage de programmation des calculatrices Texas Instrument.

   

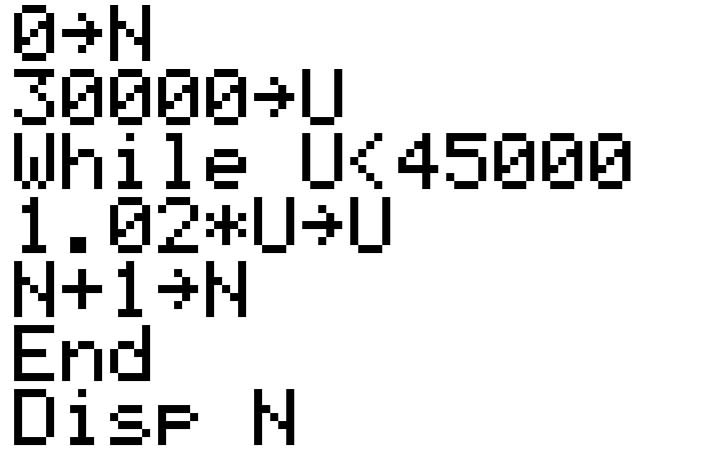
   Après exécution, le programme affiche la valeur $21$ ce qui correspond à l’année $2014 + 21 = 2035$. Donc la somme initiale aura augmenté de $50\%$ en 2035.

   
   

   Méthode 2. En déterminant la formule explicite de $(u_n)$

   Pour tout entier naturel $n$, $\; u_{n + 1} = 1{,}02u_n$. $(u_n)$ est donc une suite géométrique de raison $\text{q} = 1{,}02$. Donc pour tout entier naturel $n$,

   $$\begin{align*} u_n &= u_0 \cdot \text{q}^n \\ &= 30\,000 \cdot 1{,}02^n \\ \end{align*}$$

   On résout ensuite l’équation $u_n \geq 45\,000$.

   	$u_n \:$	$\geq 45\,000$
   $\iff \quad$	$30\,000 \cdot 1{,}02^n \:$	$\geq 45\,000$
   $\iff \quad$	$1{,}02^n \:$	$\geq \dfrac{45\,000}{30\,000}$
   $\iff \quad$	$1{,}02^n \:$	$\geq 1{,}5$
   $\iff \quad$	$\ln(1{,}02^n) \:$	$\geq \ln(1{,}5)$
   $\iff \quad$	$n\cdot \ln(1{,}02) \:$	$\geq \ln(1{,}5)$
   $\iff \quad$	$n \:$	$\geq \dfrac{\ln(1{,}5)}{\ln(1{,}02)}$

   Or :

   $$\begin{align*} \frac{\ln(1{,}5)}{\ln(1{,}02)} &= 20{,}47 \cdots \\ &\simeq 20{,}5 \quad(\text{Arrondi à }0{,}1) \\ \end{align*}$$

   L’entier directement supérieur à $20{,}5$ est $21$. Donc la somme disponible dépassera $45\,000$ à partir de la 21ème année de placement c’est-à-dire en 2035.

   On peut vérifier simplement :

   $$\begin{align*} u_{20} &= 30\,000 \cdot 1{,}02^{20} \\ &\simeq 44\,578 \quad (\text{Arrondi à l'unité})\\ \end{align*}$$

   $$\begin{align*} u_{21} &= 30\,000 \cdot 1{,}02^{21} \\ &\simeq 45\,470 \quad (\text{Arrondi à l'unité})\\ \end{align*}$$

Suite arithméticogéométrique, limite

Soit $(u_n)$ la suite définie par $u_0 = 3$ et pour tout entier naturel $n$, $\quad u_{n+1} = 0{,}5u_n + 4.$ On a représenté ci-dessous ses six premiers termes.

1. Calculer les valeurs exactes de $u_1$, $u_2$ et $u_3$.

   Réponse attendue

   $$\begin{align*} u_1 &= 0{,}5u_0 + 4 \\ &= 0{,}5 \cdot 3 + 4 \\ &= 5{,}5 \\ \end{align*}$$

   
   

   $$\begin{align*} u_2 &= 0{,}5u_1 + 4 \\ &= 0{,}5 \cdot 5{,}5 + 4 \\ &= 6{,}75 \\ \end{align*}$$

   
   

   $$\begin{align*} u_3 &= 0{,}5u_2 + 4 \\ &= 0{,}5 \cdot 6{,}75 + 4 \\ &= 7{,}375 \\ \end{align*}$$

2. Soit $(v_n)$ la suite définie pour tout entier naturel $n$ par $v_n = u_n - 8$.

   1. Démontrer que la suite $(v_n)$ est géométrique. Précisez sa raison et son premier terme.

      Réponse attendue

      D’après l’énoncé, pour tout entier naturel $n$,

      • $v_n = u_n - 8$ et
      • $u_{n+1} = 0{,}5u_n + 4$

      Donc :

      $$\begin{align*} v_{n + 1} &= u_{n + 1} - 8 \\ &= 0{,}5u_n + 4 - 8 \\ &= 0{,}5u_n - 4 \\ &= 0{,}5 \left(u_n - \frac{4}{0{,}5}\right) \\ &= 0{,}5 \left(u_n - 8\right) \\ &= 0{,}5 v_n \\ \end{align*}$$

      Donc $(v_n)$ est une suite géométrique de raison $\text{q} = 0{,}5$. Par ailleurs :

      $$\begin{align*} v_0 &= u_0 - 8 \\ &= 3 - 8 \\ &= - 5 \\ \end{align*}$$

   2. Exprimer $v_n$ en fonction de $n$.

      Réponse attendue

      D’après la question précédente, $(v_n)$ est la suite géométrique de raison $\text{q} = 0{,}5$ et de premier terme $v_0 = -5$. Donc pour entier naturel $n$ :

      $$\begin{align*} v_n &= v_0 \cdot \text{q}^n \\ &= -5 \cdot 0{,}5^n \\ \end{align*}$$

   3. En déduire que pour tout entier naturel $n$, $\quad u_n = -5 \times 0{,}5^n + 8$.

      Réponse attendue

      Pour tout entier naturel $n$,

      	$v_n \:$	$= u_n - 8$
      $\iff \quad$	$u_n \:$	$= v_n + 8$
      $\quad$	$\:$	$= -5 \cdot 0{,}5^n + 8$

   4. En déduire la limite de la suite $(u_n)$.

      Réponse attendue

      $0 < 0{,}5 < 1$ donc $0{,}5^n$ a pour limite $0$. Donc par opérations sur les limites, $(u_n)$ a pour limite $8$.

      Remarque. Ce dernier résultat est cohérent avec le graphique donnée en début d’énoncé.

Probabilités conditionnelles

On considère l’arbre de probabilité ci-dessous.

1. Recopier et compléter cet arbre.

   Réponse attendue

   On complète l’arbre en respectant la loi des noeuds.

   

2. Déterminer $P(A \cap B)$.

   Réponse attendue

   $$\begin{align*} P(A \cap B) &= P(A) \cdot P_A(B) \\ &= 0{,}8 \cdot 0{,}4 \\ &= 0{,}32 \\ \end{align*}$$

3. Montrer que $P(B) = 0{,}46$.

   Réponse attendue

   On commence par calculer $P \left(\overline{A} \cap B \right)$ :

   $$\begin{align*} P \left(\overline{A} \cap B \right) &= P \left(\overline{A} \right) \cdot P_A(B) \\ &= 0{,}2 \cdot 0{,}7 \\ &= 0{,}14 \\ \end{align*}$$

   Et ensuite, d’après la formule des probabilités totales :

   $$\begin{align*} P (B) &= P(A \cap B) + P \left(\overline{A} \cap B \right) \\ &= 0{,}32 + 0{,}14 \\ &= 0{,}46 \\ \end{align*}$$

4. Déterminer $P_B(A)$. Arrondir à $10^{-3}$ près.

   Réponse attendue

   $$\begin{align*} P_B(A) &= \frac{P(A \cap B)}{P(B)} \\ &= \frac{0{,}32}{0{,}46} \\ &= 0{,}6956 \cdots \\ &\simeq 0{,}696 \quad (\text{Arrondi à }10^{-3}) \\ \end{align*}$$

5. Facultatif. Déterminer $P(A \cup B)$.

   Réponse attendue

   $$\begin{align*} P(A \cup B) &= P(A) + P(B) - P(A \cap B) \\ &= 0{,}8 + 0{,}46 - 0{,}32 \\ &= 0{,}94 \\ \end{align*}$$

Probabilités : lois binomiales

Dans un club de sport, Julien joue au Basket. Il sait que lors d’un lancer, sa probabilité de marquer un panier est égale à $0{,}6$.

1. Julien lance le ballon quatre fois de suite. Les quatre lancers sont indépendants les uns des autres. On note $X$ la variable aléatoire associant à chaque série de de quatre lancers le nombre de paniers marqués par Julien.

   1. Justifier que $X$ suit un loi binomiale dont on précisera les paramètres.

      Réponse attendue

      Les quatre lancers sont indépendants et à chaque lancer, la probabilité de marquer un panier est égale à $0{,}6$. Donc $X$ suit la loi binomiale de paramètres $n = 4$ et $p = 0{,}6$.

   2. Montrer que $P(X = 0) = 0{,}0256$ et interpréter ce résultat.

      Réponse attendue

      $$\begin{align*} P(X = 0) &= \binom{4}{0} \cdot 0{,}6^0 \cdot 0{,}4^4 \\ &= 1 \cdot 1 \cdot 0{,}4^4 \\ &= 0{,}4^4 \\ &= 0{,}0256 \\ \end{align*}$$

      Donc la probabilité que Julien rate quatre lancers de suite est égale à $0{,}0256$. Formulation alternative. Sur quatre lancers successifs, Julien a $2{,}56\%$ de chance de rater tous ses lancers.

   3. Calculer $P(X \geqslant 1)$ et interpréter le résultat.

      Réponse attendue

      L’événement $(X \geqslant 1)$ signifie “Julien marque au moins un panier sur les quatre lancers successifs.”. C’est l’événement contraire de $(X = 0)$ signifiant “Julien ne marque aucun panier sur les quatre lancers successifs.”. On a donc :

      $$\begin{align*} P(X \geqslant 1) &= 1 - P(X = 0) \\ &= 1 - 0{,}0256 \\ &= 0{,}9744 \\ \end{align*}$$

      Donc la probabilité que Julien marque au moins un panier sur quatre lancers successifs est égale à $0{,}9744$. Formulation alternative. Sur quatre lancers successifs, Julien a $97{,}44\%$ de chance de marquer au moins un lancer.

   4. Calculer l’espérance de $X$ et interpréter le résultat.

      Réponse attendue

      $$\begin{align*} E(X) &= n \cdot p \\ &= 4 \cdot 0{,}6 \\ &= 2{,}4 \\ \end{align*}$$

      Donc sur une série de quatre lancers successifs, Julien marque en moyenne $2{,}4$ lancers.

2. Facultatif. Combien de fois Julien doit-il lancer le ballon au minimum pour que la probabilité qu’il marque au moins un panier soit supérieure à $0{,}999$ ?

   Réponse attendue

   Soit $n$ le nombre de lancers successifs réalisés par Julien. Soit $Y$ la variable aléatoire associant à chaque série de $n$ lancers le nombre de paniers marqués. Selon les hypothèses de l’énoncé, $Y$ suit une loi de paramètres $n$ ($n$ étant un entier naturel) et $p = 0{,}6$. On a donc :

   $$\begin{align*} P(Y = 0) &= \binom{n}{0} \cdot 0{,}6^0 \cdot 0{,}4^n \\ &= 1 \cdot 1 \cdot 0{,}4^n \\ &= 0{,}4^n \\ \end{align*}$$

   Et en suivant le même raisonnement qu’à la question 1.c., on obtient :

   $$\begin{align*} P(Y \geqslant 1) &= 1 - P(Y = 0) \\ &= 1 - 0{,}4^n \\ \end{align*}$$

   On résout maintenant l’équation $P(Y \geqslant 1) \geqslant 0{,}999$.

   	$P(Y \geqslant 1) \:$	$\geqslant 0{,}999$
   $\iff \quad$	$1 - 0{,}4^n \:$	$\geqslant 0{,}999$
   $\iff \quad$	$- 0{,}4^n \:$	$\geqslant -0{,}001$
   $\iff \quad$	$0{,}4^n \:$	$\leqslant 0{,}001$
   $\iff \quad$	$\ln(0{,}4^n) \:$	$\leqslant \ln(0{,}001)$
   $\iff \quad$	$n\cdot \ln(0{,}4) \:$	$\leqslant \ln(0{,}001)$
   $\iff \quad$	$n \:$	$\geqslant \dfrac{\ln(0{,}001)}{\ln(0{,}4)}$	$\quad\quad(\text{Car }\ln(0{,}4) < 0)$

   Or:

   $$\begin{align*} \dfrac{\ln(0{,}001)}{\ln(0{,}4)} &= 7{,}53 \cdots \\ &\simeq 7{,}5 \quad (\text{Arrondi à }0{,}1) \\ \end{align*}$$

   L’entier directement supérieur à $7{,}5$ est $8$. Donc Julien doit lancer au minimum huit fois le ballon pour que la probabilité qu’il marque au moins un panier soit supérieure à $0{,}999$.

   On peut vérifier simplement :

   • Pour $n = 7$ :

   $$\begin{align*} P(Y \geqslant 1) &= 1 - 0{,}4^7 \\ &= 0{,}9983 \cdots \\ &< 0{,}999 \\ \end{align*}$$

   • Pour $n = 8$ :

   $$\begin{align*} P(Y \geqslant 1) &= 1 - 0{,}4^8 \\ &= 0{,}9993 \cdots \\ &\geqslant 0{,}999 \\ \end{align*}$$

Exercices de spécialité

Matrices et systèmes d’équation

Une entreprise fabrique trois modèles d’ordinateur :

• Bas de Gamme (BG)
• Moyenne Gamme (MG)
• Haut de Gamme

Le tableau ci-dessous indique le nombre d’unités nécessaires à la fabrication de chaque modèle.

Modèle	BG	MG	HG
Unités de composants	$3$	$5$	$9$
Unités d’assemblage	$1$	$1$	$2$
Unités de recherche	$1$	$2$	$3$

Ainsi, par exemple, la fabrication d’un ordinateur BG demande trois unités de composants, une unité d’assemblage et une unité de recherche.

1. Déterminer le nombre d’unités nécessaires pour construire au total :

   • $5$ ordinateurs BG
   • $4$ ordinateurs MG
   • $3$ ordinateurs HG
   Réponse attendue

   On utilise le tableau ci-après pour calculer le nombre d’unités nécessaires pour fabriquer :

   • $\textbf{5}$ ordinateurs BG ;
   • $\textbf{4}$ ordinateurs MG ;
   • $\textbf{3}$ ordinateurs HG.

   Modèle	BG	MG	HG	Nombre total d’unités
   Unités de composants	$3 \cdot \textbf{5}$	$5 \cdot \textbf{4}$	$9 \cdot \textbf{3}$	$63$
   Unités d’assemblage	$1 \cdot \textbf{5}$	$1 \cdot \textbf{4}$	$2 \cdot \textbf{3}$	$15$
   Unités de recherche	$1 \cdot \textbf{5}$	$2 \cdot \textbf{4}$	$3 \cdot \textbf{3}$	$22$

   Donc, il faut :

   • $63$ unités de composantes
   • $15$ unités d’assemblage
   • $22$ unités de recherche

   Remarque

   Le calcul précédant correspond en fait au calcul matriciel suivant :

   $$\begin{equation*} \begin{pmatrix} 3 & 5 & 9 \\[3pt] 1 & 1 & 2 \\[3pt] 1 & 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} 5 \\[3pt] 4 \\[3pt] 3 \end{pmatrix} \end{equation*}$$	$$\begin{equation*} \, = \left( \begin{array} 33 \cdot 5 &+& 5 \cdot 4 &+& 9 \cdot 3 \\[3pt] 1 \cdot 5 &+& 1 \cdot 4 &+& 2 \cdot 3 \\[3pt] 1 \cdot 5 &+& 2 \cdot 4 &+& 3 \cdot 3 \end{array} \right) \end{equation*}$$
   $$\begin{equation*} \end{equation*}$$	$$\begin{equation*} \, = \begin{pmatrix} 63 \\[3pt] 15 \\[3pt] 22 \end{pmatrix} \end{equation*}$$

2. Calculer le nombre d’ordinateurs fabriqués de chaque modèle si l’entreprise utilise exactement :

   • $920$ unités de composantes
   • $230$ unités d’assemblage
   • $330$ unités de recherche
   Réponse attendue

   On note :

   • $x$ le nombre d’ordinateurs BG fabriqués
   • $y$ le nombre d’ordinateurs MG fabriqués
   • $z$ le nombre d’ordinateurs HG fabriqués

   On traduit ensuite la situation par un tableau :

   Modèle	BG	MG	HG	Nombre total d’unités
   Unités de composants	$3 \cdot x$	$5 \cdot y$	$9 \cdot z$	$920$
   Unités d’assemblage	$1 \cdot x$	$1 \cdot y$	$2 \cdot z$	$230$
   Unités de recherche	$1 \cdot x$	$2 \cdot y$	$3 \cdot z$	$330$

   Le problème se ramène donc au système d’équations suivant.

   $$\begin{cases} \begin{array}{rcrcrcl} 3x& + &5y& + &9z &=& 920 \\[4pt] x& + &y& + &2z &=& 230 \\[4pt] x& + &2y& + &3z &=& 330 \end{array} \end{cases}$$

   Ce système est équivalent à l’équation matricielle suivante :

   $$\begin{equation*} \begin{pmatrix} 3 & 5 & 9 \\[3pt] 1 & 1 & 2 \\[3pt] 1 & 2 & 3 \end{pmatrix} \cdot \begin{pmatrix} x \\[3pt] y \\[3pt] z \end{pmatrix} = \end{equation*}$$

   $$\begin{equation*} \, \begin{pmatrix} 920 \\[3pt] 230 \\[3pt] 330 \end{pmatrix} \end{equation*}$$

   Ensuite on pose :

   $$\begin{equation*} \quad \begin{pmatrix} 3 & 5 & 9 \\[3pt] 1 & 1 & 2 \\[3pt] 1 & 2 & 3 \end{pmatrix} = A \quad \end{equation*}$$

   $$\begin{equation*} \quad \begin{pmatrix} x \\[3pt] y \\[3pt] z \end{pmatrix} = X \quad \end{equation*}$$

   $$\begin{equation*} \quad \begin{pmatrix} 920 \\[3pt] 230 \\[3pt] 330 \end{pmatrix} = B \quad \end{equation*}$$

   On entre dans la calculatrice les matrices $A$ et $B$. Ensuite, à la calculatrice on détermine que :

   $$\begin{equation*} A^{-1} = \begin{pmatrix} -1 & 3 & 1 \\[3pt] -1 & 0 & 3 \\[3pt] 1 & -1 & -2 \end{pmatrix} \end{equation*}$$

   Avec les notations précédentes on peut donc écrire et trouver à la calculatrice :

   	$$\begin{equation*} A \cdot X \, \end{equation*}$$	$$\begin{equation*} = B \end{equation*}$$
   $$\begin{equation*} \iff\quad \end{equation*}$$	$$\begin{equation*} \color{white}{A^{-1}} X \, \end{equation*}$$	$$\begin{equation*} = A^{-1} \cdot B \end{equation*}$$
   		$$\begin{equation*} = \begin{pmatrix} 100 \\[3pt] 70 \\[3pt] 30 \end{pmatrix} \end{equation*}$$

   En conclusion, l’entreprise a fabriqué :

   • $100$ ordinateurs BG
   • $70$ ordinateurs MG
   • $30$ ordinateurs HG

Graphe, généralités et parcours optimal

Deux groupes d’amis organisent une randonnée dans les Alpes. On a représenté par le graphe ci-dessous les sommets $B$, $C$, $D$, $F$, $T$ et $N$ par lesquels ils peuvent choisir de passer. Une arête entre deux sommets coïncide avec l’existence d’un chemin entre deux sommets.

1. Dans un tableau indiquer le degré de chaque sommet.

   Réponse attendue

   Dans un graphe, le degré d’un sommet est le nombre d’arête dont ce sommet est une extrémité. On en déduit :

   Sommet	$B$	$C$	$D$	$F$	$T$	$N$
   Degré	$2$	$4$	$4$	$5$	$4$	$3$

2. Justifier que le graphe est connexe.

   Réponse attendue

   Ce graphe est connexe car pour tout couple de sommets de ce graphe, ces deux sommets peuvent être reliés par une chaîne.

3. Le premier groupe souhaite passer par les six sommets en passant une fois et une seule par chaque chemin.

   1. Démontrer que leur souhait est réalisable.

      Réponse attendue

      D’après la question 1., le graphe étudié possède exactement deux sommets de degré pair et est un graphe connexe. Donc d’après le théorème d’Euler, ce graphe contient une chaîne eulérienne. Une chaîne eulérienne est une chaîne passant par toutes les arêtes du graphe.

      Donc le souhait du premier groupe est réalisable.

   2. Donner un exemple de trajet possible.

      Réponse attendue

      Un exemple de trajet possible :

      $F - B - C - F - D - T - C - D - N - F - T - N$

4. Les distances en kilomètres entre chaque sommet ont été ajoutées sur le graphe ci-dessous.

   

   Le second groupe se trouve au sommet $B$ et souhaite se rendre au sommet $N$. À l’aide d’un algorithme, indiquer une chaîne qui minimise la distance du trajet.

   Réponse attendue

   On utilise l’algorithme de Dijkstra (à prononcer approximativement “Dextra”).

   Étape	$B$	$C$	$F$	$T$	$D$	$N$
   $1$	$\color{white}{0}0_{\color{white}{A}}$	$12_B$	$15_B$
   $2$	X	$\color{red}{12_B}$	$15_C$	$17_C$	$14_C$
   $3$	X	X	$18_D$	$17_D$	$\color{red}{14_C}$	$26_D$
   $4$	X	X	$\color{red}{15_B}$	$23_F$	X	$38_F$
   5	X	X	X	$\color{red}{17_C}$	X	$24_T$
   6	X	X	X	X	X	$\color{red}{24_T}$

   La chaîne qui minimise la distance du trajet est donc $B-C-T-N$ avec un total de 24 km.

   Remarque. En fait dans le tableau présentant l’exécution de l’algorithme de Dijkstra, on a fait des choix arbitraires. En effet, à l’étape $4$ dans la colonne $F$ on a choisit $\color{red}{15_B}$ alors que $15_C$ était également possible. De même, à l’étape $5$ on a choisit $\color{red}{15_B}$ alors que $17_D$ était également possible. Donc la chaîne $B - C - D - T - N$ était également possible. Cela n’a pas d’incidence sur le résultat en terme de distance puisque l’on obtient également une distance de 24 km.

Graphe probabiliste et matrices

Karine écoute chaque jour du Jazz ou du Rock sur le trajet entre son domicile et son lieu de travail. Si elle écoute du Jazz un jour, la probabilité qu’elle écoute à nouveau du jazz le lendemain est égale à $0{,}85$. Si elle écoute du Rock un jour, la probabilité qu’elle écoute du Rock le lendemain est égale à $0{,}98$.

1. Reproduire et compléter le graphe ci-dessous traduisant la situation.

   
   Réponse attendue

   

2. Donner la matrice de transition $M$ associée à cette situation (Prendre dans l’ordre Jazz puis Rock).

   Réponse attendue

   $M\,$

   $$\begin{equation*} = \left( \begin{array} 00{,}85 & 0{,}15 \\[3pt] 0{,}02 & 0{,}98 \end{array} \right) \end{equation*}$$

3. On est lundi. Karine écoute du jazz. Quelle est la probabilité qu’elle écoute du jazz le mercredi suivant ?

   Réponse attendue

   Au départ, le lundi, Karine écoute du jazz donc l’état initial du graphe est :

   $$\begin{equation*} P_0 = \begin{pmatrix} 0{,}85 & 0{,}15 \end{pmatrix} \end{equation*}$$

   L’état du graphe, le mercredi, c’est-à-dire deux jours plus tard est :

   $P_2 \,$	$= P_0 M^2$
   	$$\begin{equation*} = \begin{pmatrix} 0{,}85 & 0{,}15 \end{pmatrix} \begin{pmatrix} 0{,}85 & 0{,}15 \\[3pt] 0{,}02 & 0{,}98 \end{pmatrix} ^2 \end{equation*}$$
   	$$\begin{equation*} \simeq \begin{pmatrix} 0{,}62 & 0{,}38 \end{pmatrix} \end{equation*}$$

   Les coefficients de $P_2$ ont été arrondis au centième. En conclusion, si le lundi Karine écoute du Jazz alors la probabilité qu’elle écoute du Jazz le mercredi suivant est d’environ 0{,}25.

   Remarque. Il est possible que l’expression “mercredi suivant” signifie le mercredi de la semaine suivante. Dans ce cas, on doit déterminer l’état du graphe 9 jours plus tard :

   $P_9 \,$	$= P_0 M^9$
   	$$\begin{equation*} = \begin{pmatrix} 0{,}85 & 0{,}15 \end{pmatrix} \begin{pmatrix} 0{,}85 & 0{,}15 \\[3pt] 0{,}02 & 0{,}98 \end{pmatrix} ^9 \end{equation*}$$
   	$$\begin{equation*} \simeq \begin{pmatrix} 0{,}25 & 0{,}75 \end{pmatrix} \end{equation*}$$

   Les coefficients de $P_9$ ont été arrondis au centième. En conclusion, si le lundi Karine écoute du Jazz alors la probabilité qu’elle écoute du Jazz le mercredi suivant est d’environ $0{,}25$.

4. Déterminer la matrice ligne $P = (a \quad b)$ où $a$ et $b$ désignent deux nombres réels positifs tels que $a + b = 1$ et $PM = P$. Que représente cette matrice $P$ ?

   Réponse attendue

   	$P M$	$\,= P$
   $\iff$	$$\begin{equation*} \begin{pmatrix} a & b \end{pmatrix} \begin{pmatrix} 0{,}85 & 0{,}15 \\[3pt] 0{,}02 & 0{,}98 \end{pmatrix} \, \end{equation*}$$	$$\begin{equation*} \, = \begin{pmatrix} a & b \end{pmatrix} \end{equation*}$$
   $\iff$	$$\begin{equation*} \left\lbrace \begin{array}{rcr} 0{,}85a& + &0{,}02b\; \\[6pt] 0{,}15a& + &0{,}98b\; \end{array} \right. \end{equation*}$$	$$\begin{equation*} \begin{array}{rr} = & a \color{white}{0{,}0}\\[6pt] = & b \color{white}{0{,}0} \end{array} \end{equation*}$$
   $\iff$	$$\begin{equation*} \left\lbrace \begin{array}{rcrcrcl} -0{,}15a& + &0{,}02b\; \\[6pt] 0{,}15a& - &0{,}02b\; \\[6pt] \end{array} \right. \end{equation*}$$	$$\begin{array}{rr} = & 0 \\[6pt] = & 0 \\[6pt] \end{array}$$
   $\iff$	$$\begin{equation*} 15a \end{equation*}$$	$$\begin{equation*} \,= 2b \end{equation*}$$

   Or d’après l’énoncé, $a + b = 1$ donc $b = 1 - a$. L’équation précédente devient donc :

   	$15a\,$	$= 2 - 2a$
   $\iff \quad$	$17a\,$	$= 2$
   $\iff \quad$	$a\,$	$= \dfrac{2}{17}$

   Donc : $$\begin{equation*} P = \begin{pmatrix} \dfrac{2}{17} & \dfrac{15}{17} \end{pmatrix} \end{equation*}$$

   La matrice ligne $P$ représente l’état stable du graphe.